
[HOME]
[WEB ALBUMS]
[PROJECTS]
[ARCHIVE]
[DOWNLOADS]
[LINKS]
PROJECTS
Project MK2: Curve fitting of neutral hydrogen profiles with Gauss curves
Here we go on with further data post processing of the project1 data
It is assumed that the neutral hydrogen gas clouds, like many natural processes can be described as a sum of Gaussian curves.
The trick is, how to break up the curve into separate Gaussian curves.
In earlier days that was done by hand with drawings and tables (In the pre PC time up to 50 volunteers were working on this Dwingeloo data). Now we can analyse the curve with a PC program.
There are several programs available on the net which work in excel.
The input is the file of the amplitude versus frequency in the range of 2 to 3 MHz. The output gives a table of Gaussian curves and parameters. If we sum the curves and the compare it to the input curve than we can see a very good match. Often a remnant error curve is made as a control.
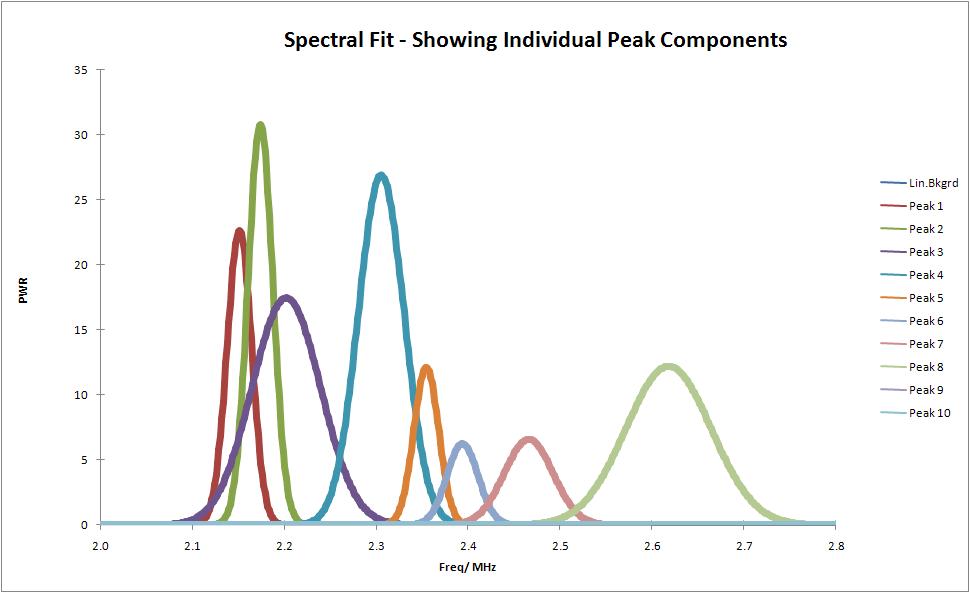
Fig.1 - Gauss Curves.
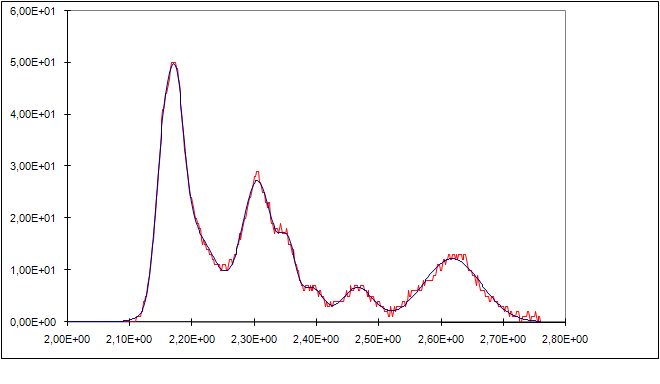
Fig.2 - Curve fit.
Obviously, the setting of the receiver and the internal oscillator have to be accounted for, so 1418.3036 MHz should be added to the above frequencies.
The three output parameters are the maximum power amplitude, its frequency in Hz and the width of each Gauss curve in Hz.
An indication of the amount of hydrogen atoms per volume can now calculated by; amplitude* FWHM value. (full width at half maximum)
The frequency can be converted into the speed difference between the observer and the cloud. We use the formula v = c * (1-f/f0), with
f0 being the hyperfine flip spin frequency of the hydrogen at 1420.405752MHz and f is the observed frequency and c is the speed of light.
But we have not taken into account the motion of the earth / and the sun itself, and our solar system in a certain direction. You can find an online calculator here https://www.astro.virginia.edu/~emm8x/utils/vlsr.html.
To correct that at a certain date and time, we must add a speed of 23km/s.
| IF out | Intensity | FWHM | F0corr | V | V-LSR | N | Rgc |
|---|
| [MHz] | [x*W] | [MHz] | [MHz] | [km/s] | [km/s] | [x*n/cm^3] | [kps] |
|---|
| 2.15 | 23 | 0.063 | 1420.4536 | -10 | 13 | 0.8 | - |
|---|
| 2.17 | 31 | 0.064 | 1420.4736 | -14 | 9 | 1.0 | - |
|---|
| 2.2 | 17 | 0.176 | 1420.5036 | -42 | -19 | 1.6 | - |
|---|
| 2.31 | 27 | 0.12 | 1420.6136 | - | - | - | - |
|---|
| 2.35 | 11 | - | - | - | - | - | - |
|---|
| 2.39 | 6 | - | - | - | - | - | - |
|---|
| 2.47 | 7 | - | - | - | - | - | - |
|---|
| 2.61 | 12 | 0.22 | 1420.9136 | -107 | -84 | 2 | 13.8 |
|---|
Fig.3 - Result Table.
The first two Gaussian curves indicate that the clouds are faster (receiding us; lower receive frequency) than us. The next curve is wide, it is the cloud that has the same speed as the solar system.
Next is the cloud we "catch up" (aproaching us) because it is outside our solar galactic circle.
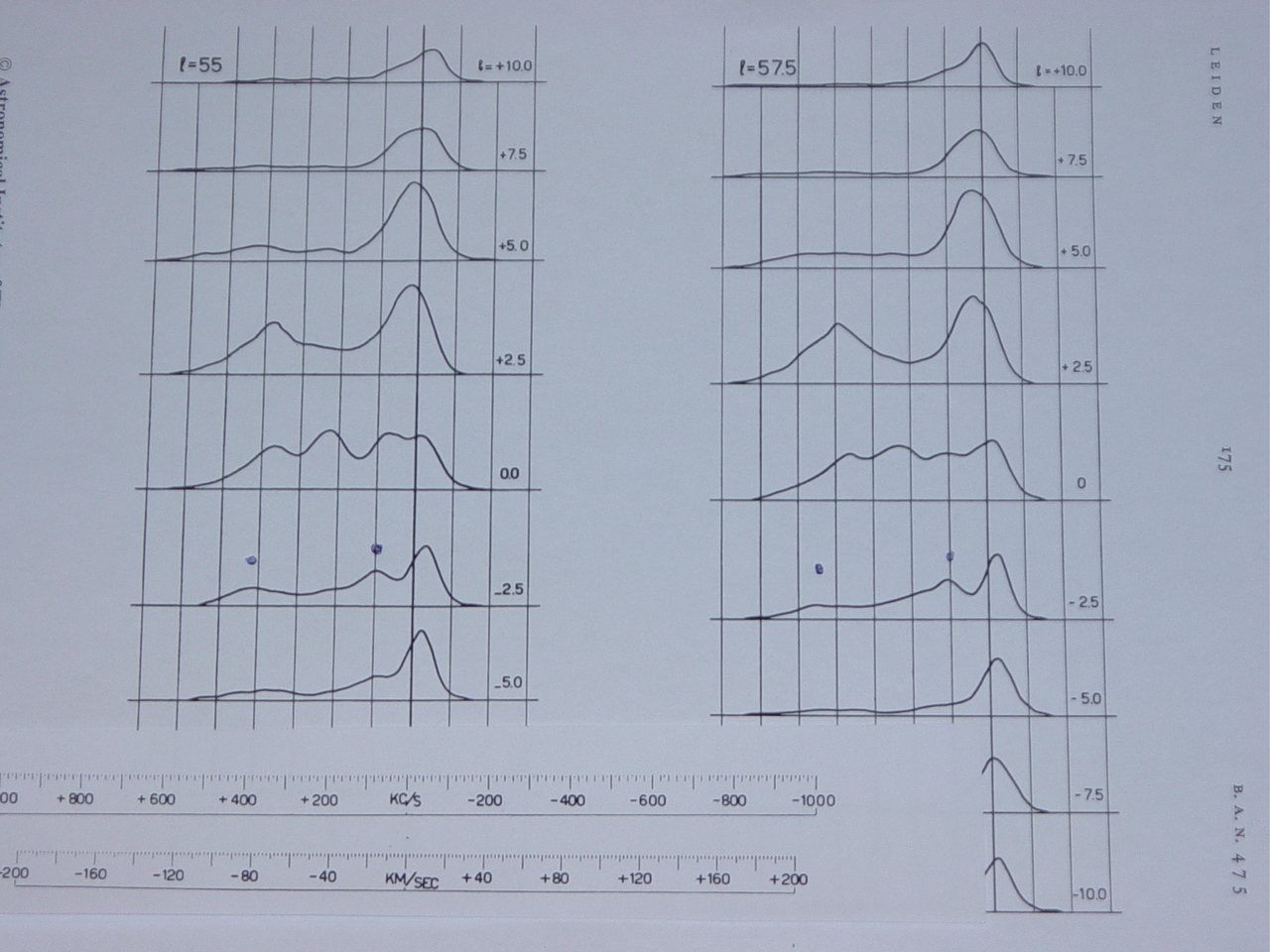
Fig.4 - Muller Westerhout (1957).
Next we want to know where the clouds are in our galaxy.
Here we have a real problem, one is not sure of the rotational speed in our as a function of distance R from the center.
Logical would be that, like the inner planets in our solar system, the inner planets rotate faster and the outer slower. In a galaxy this appears to be different.
The speed of the gas in most part of the galaxy disk rotates with thesame speed, however, because the outer clouds have to travel a long way to go around than the centre clouds.
At championships they take this into account and the athletes do not start on a row at the start.
Nowadays it is assumed that the radial velocity between 5 and 15 kpc is approximately equal to 220 km / s. This result is among others due to optical observations.
The location of the sun is 8.5 kpc (kilo parsec)from the galactic center. (1kpc = 3 * 10 ^ 16 km)
As previously reported, the dish was pointed at L = 88.3517, b = -1.787. For convenience, we round off the galactic latitude of 90 degrees.
With a little geometry, we can now say that R0/R1 = (V0-Vd) / V1.
Here R0 is the distance from the Sun to the galactic center.
V0 is our own rotational speed = 220 km/s. R1 is the distance from the cloud to the galactic center.
Vd is the difference in speed between the Sun and the cloud (see above).
V1 is the rotational speed of the cloud around the galactic center. (= 220 km/s)
For the cloud with the largest velocity difference of 84 kilometers/s we get at a distance of 13.8 kpc from the center.
Next we can compare the curve with the literature, for instance the measurements of Muller and Westerhout (1957), and we see that they measured 12kpc.
This is somewhat different, but the constant rotation speed was not yet known.
So the galaxy appears to be greater than previously thought.
Michiel Klaassen 18-05-2012




